Las Griegas: VEGA, sensibilidad a la Volatilidad Implícita.

La cuarta y última griega de la que vamos a hablar es Vega. En artículos anteriores hemos hablado de las griegas Delta, Gamma y Theta.

Tal y como comentamos cuando hablamos de la griega Theta, debemos tener en cuenta que el precio de las opciones se divide en dos componentes:

• Valor extrínseco
• Valor intrínseco

Al valor extrínseco se le conoce también como “time value” y será 0 al vencimiento de la opción. Pues bien, la griega Vega sólo afecta a este valor extrínseco, nunca al valor intrínseco de la opción.

Por pura definición, Vega mide los cambios en el precio de una opción en relación con cambios de un 1% en la volatilidad implícita de dicha opción (No confundir con la volatilidad implícita del activo subyacente al que pertenece dicha opción), cambiando así su valor teórico (valor Extrínseco + Valor Intrínseco). Nos referimos a que la volatilidad pase por ejemplo de un 10% a un 11%, o de un 20% a un 19%.

Los operadores de opciones eligieron usar el término Vega ya que la letra V de «Vega» les recuerda a la volatilidad.

Vega es siempre un importe positivo tanto para opciones Calls como para opciones Puts el cual se expresa en forma de número entero (puede haber algunos softwares que lo representen en número decimal). Este importe representa la modificación del importe en efectivo de una opción y, por tanto, una opción con una cantidad Vega de 200 subirá o bajará ese importe en su valoración por cada punto porcentual que varíe su volatilidad implícita, partiendo siempre de que todos los demás factores se mantuvieran constantes. De esta forma, la griega Vega traduce la volatilidad implícita de una opción en dinero.

Como hemos comentado, Vega sólo afecta al valor extrínseco de la opción y como las opciones ATM (At the Money) tienen el mayor valor extrínseco, la Vega será más alta para estas opciones, disminuyendo según nos alejemos del dinero, es decir, para las opciones OTM e ITM.

Es importante resaltar que Vega puede ser la griega más importante para determinar el precio de la opción y la más difícil de entender. No obstante, esta griega es mucho más importante para los traders profesionales o que realicen estrategias avanzadas que para los retails o principiantes.

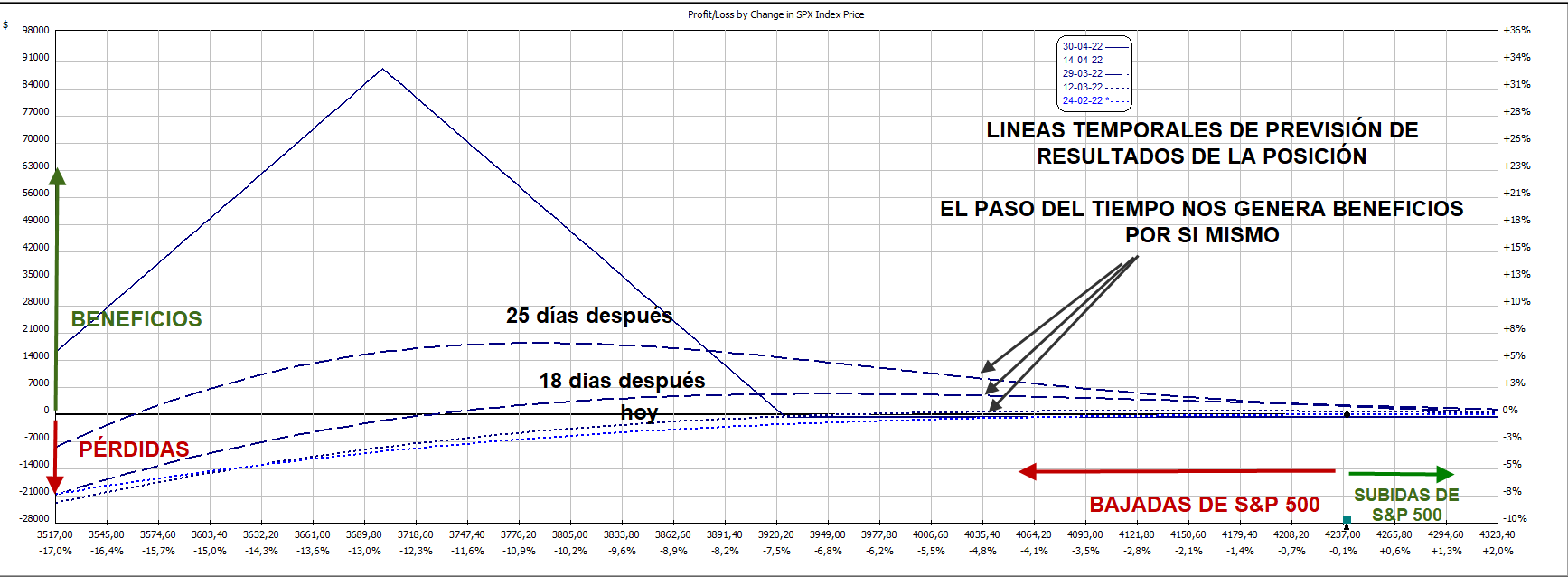
De una forma general, se puede argumentar que cuando sube o baja la volatilidad el precio de la opción, de igual forma, sube o baja. Por este mismo razonamiento, como la Volatilidad va en aumento a medida que la opción esté más alejada de su fecha de vencimiento (más incertidumbre), el precio de las opciones será más caro cuanto más días queden para su expiración.

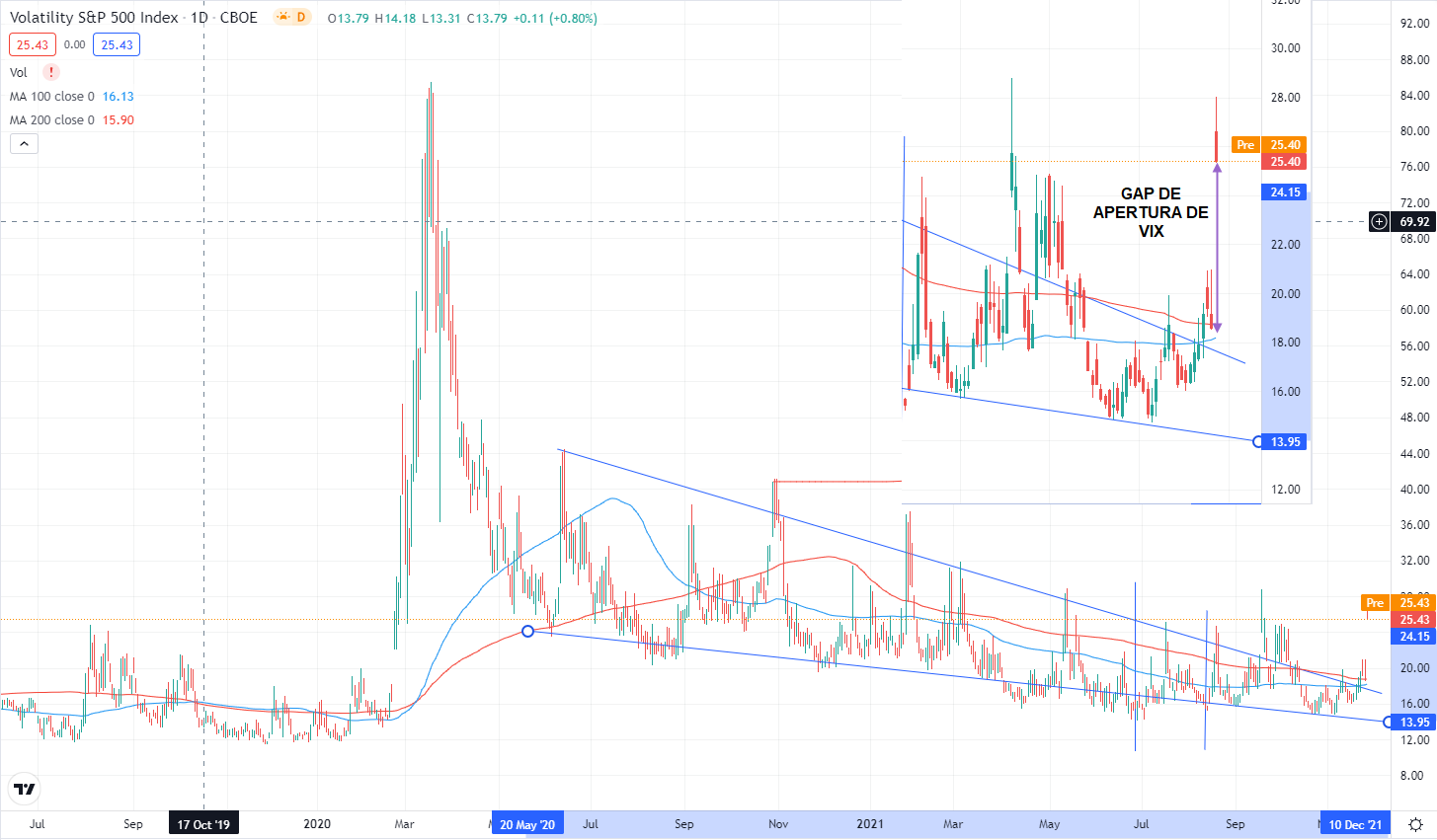
Otra forma de verlo, es que se puede entender la volatilidad implícita de un activo subyacente como la probabilidad de que éste alcance cualquier nivel de precio en un período determinado. Por tanto, a más tiempo a vencimiento de la opción más probable es que el dicho nivel sea alcanzado pues el mercado tendría más tiempo para ello. Por ese motivo, a más tiempo hasta vencimiento mayor es el precio de una opción para un mismo tipo y strike. Se puede apreciar en la siguiente imagen:

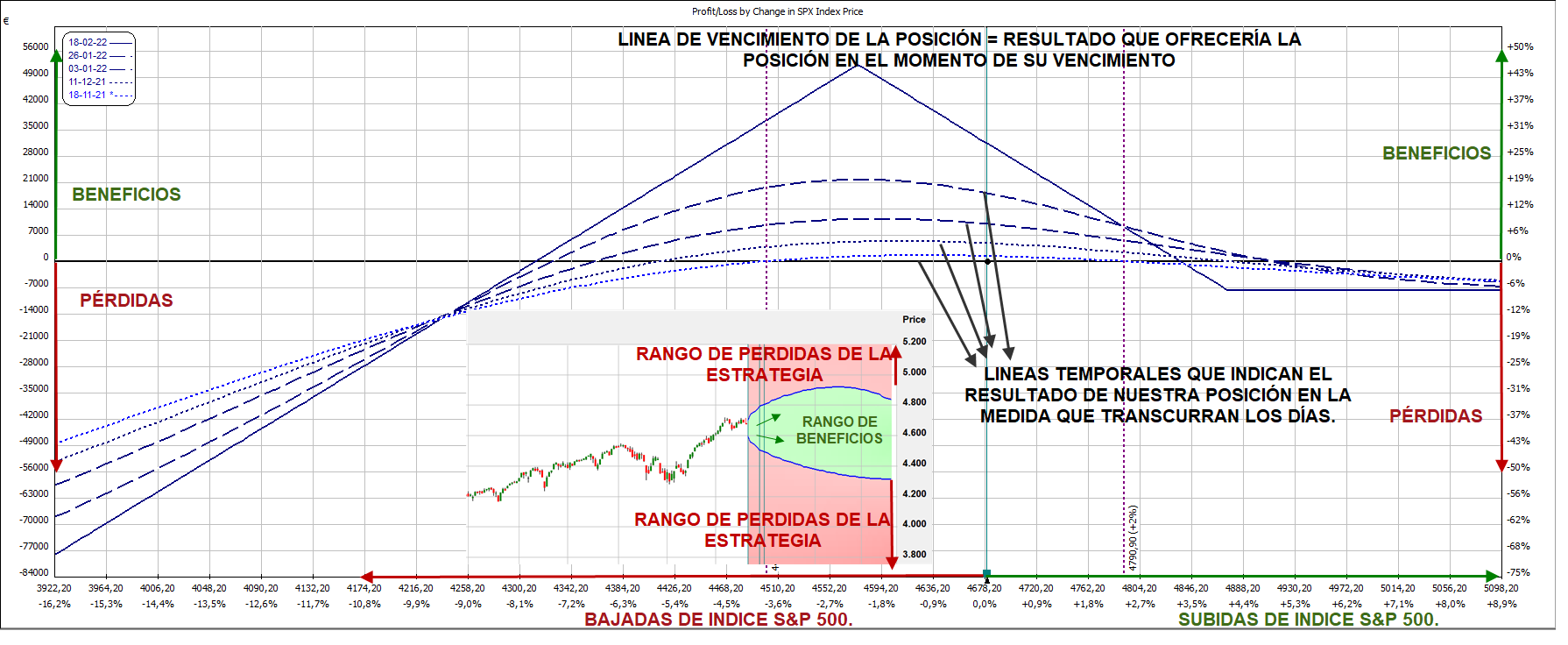
Derivado de esto, otra característica a tener en cuenta es que una opción Call y una opción Put del mismo strike y vencimiento tendrán el mismo valor de Vega, es decir, Vega es prácticamente idéntica para Call y Put tal y como se puede apreciar en el siguiente gráfico:

Vega decrece mucho cuando se acerca la fecha de expiración de la opción. Esto se debe a que, al quedar cada vez menos tiempo para el vencimiento, es cada vez más difícil que la volatilidad implícita pueda afectar de forma significativa al valor extrínseco de la opción.

Para entender bien cómo funciona Vega, necesitamos revisar rápidamente los modelos de precios de las opciones:

Los modelos de fijación de precios para las opciones son fórmulas matemáticas que ayudan a los inversores a eliminar las conjeturas a la hora de determinar el precio de cada opción. Los modelos hacen algunas suposiciones; entre ellas, que las cotizaciones bursátiles de los activos subyacentes son aleatorias y que sólo una de las cuatro griegas de las opciones cambiará en un momento dado.

El modelo Black Scholes desarrollado en 1973 es el más conocido de los modelos de fijación de precios de las opciones. Los modelos subsiguientes se han desarrollado a lo largo del tiempo para corregir algunas de las imprecisiones de este modelo inicial como la suposición de una volatilidad constante, distribuciones log-normal y no tener en cuenta el ejercicio anticipado de las opciones y dividendos al estilo americano. Mientras que modelos como éstos ayudan a los inversionistas a determinar los precios, es importante entender que ningún modelo puede replicar completamente todos los factores que determinan el precio de una opción en el mundo real. Simplemente aportan un precio de referencia a considerar más o menos acertado.

En realidad y a efectos prácticos la volatilidad implícita de las opciones viene determinada por la evaluación que hace el creador de mercado -market maker- de las expectativas del público con respecto a eventos que podrían cambiar el valor de una opción, es decir, de la incertidumbre futura percibida y cotizada por el mercado.

Los creadores de mercado, como proveedores obligados de liquidez, tienen la obligación de vender opciones a los compradores de éstas. Por ese motivo tienden a aumentar el precio de las opciones y con ello su volatilidad implícita cuando perciben fuertes demandas de opciones. De esta forma, obtienen un mayor beneficio al realizar su labor. Por el contrario, cuando el mercado está vendiendo opciones, estos creadores de mercado encargados de la obligación de comprar a estos vendedores, bajan el precio de las opciones al bajar sus valoración y volatilidad implícita. Esta es también la razón por la que la volatilidad implícita de los mercados de renta variable tiende a aumentar en un mercado bajista y a caer en un mercado alcista.

Hay que tener en cuenta que los inversores institucionales gestionan sus posiciones de volatilidad e intercambian sus cotizaciones no a través de los precios de las opciones, sino a través de la Volatilidad Implícita de las opciones. Utilizan transformaciones de los modelos conocidos (BMS Black-Merton-Scholes) para mejorar la estabilidad de las cotizaciones y resaltar la información de los contratos de opciones, obteniendo así mucha más confianza en la evolución de la Volatilidad implícita tanto en el corto como en el muy largo plazo.

Relación Vega – Theta.

La letra griega Vega tiene un valor de signo contrario a Theta (Vega tiene un valor positivo y Theta tiene un valor negativo). Para los vendedores de opciones, Vega representa el riesgo por incrementos en la volatilidad y Theta es lo que aproximadamente se depreciará el precio de la opción por cada día de negociación que transcurra.

Por tanto, es necesario mantener una posición equilibrada de estas dos griegas. Cuando esta relación es demasiado alta, la volatilidad tendrá un gran impacto en nuestra posición, y lo que necesitamos como income traders de opciones es que Theta sea el principal motor de nuestra posición.

Con respecto a la relación que pueda tener este ratio (ratio Risk/Return), cada operador puede tener sus preferencias. No obstante, una buena regla empírica es mantener este ratio Vega/Theta por debajo de 4, es decir, que Vega no sea mayor que cuatro veces Theta, aunque cuanto más baja sea esta relación más seguro y robusta será la posición.

Esto tiene su lógica en que el mercado suele permanecer lateralizado el 80% del tiempo siendo aproximadamente sólo un 20% en el que se mueve de forma tendencial. Por este motivo es conveniente que Vega sea máximo 4 veces el valor de Theta. Así grosso modo 4 días de Theta nos compensarían el movimiento en contra de un punto de incremento de volatilidad.

Relación Volatilidad Implícita y Volatilidad Histórica.

Hay que tener en cuenta la relación entre la Volatilidad implícita (VI) y la Volatilidad Histórica (VH), o realizada. La VH es un dato conocido ya que se calcula mediante la variación que ha tenido el rendimiento del activo en un cierto periodo de tiempo, generalmente en los últimos 30 días.

Como regla general y básica, se puede decir que si VI > VH las opciones están caras y es buen momento para venderlas. Si por el contrario la VI < VH, las opciones están baratas y es buen momento para comprarlas.

Generalmente las VI será mayor que la VH o realizada, y su diferencia se la llama la “Prima de Riesgo de Volatilidad” (VRP) que puede ser visto como la prima que los vendedores de opciones reciben de los compradores de opciones que buscan una forma de seguro financiero contra incrementos de volatilidad. Esta prima, o costo, cubre al vendedor hasta cierto punto si el precio del subyacentes se mueve en una dirección desfavorable para su posición. Sin esta prima, los vendedores de opciones no tendrían realmente ningún incentivo para entrar en el mercado.

Históricamente, las opciones sobre índices bursátiles han mostrado un VRP positivo en más del 85% de los casos desde 1990.

Dependiendo de la diferencia que pueda existir entre ambas magnitudes -VH vs VI-, podemos apreciar el grado de sobrevaloración de las opciones que tenemos en cartera o que nos disponemos a operar.

Mis mejores deseos.